As announced in Newsletter 4, the Investment
Science web site is up. It is located at
http://www.investmentscience.com. There has been a good deal of
activity at the site, and we have plans to add more to it. For one
thing, you will find copies of all past issues of this Newsletter
at the site and some very useful software (see below). Your
comments on the site are welcome.
An Excel add-in for drawing and evaluating
triangular lattices was developed by José Carlos García Franco. We
have used a version of this in the short course and we use it often
to carry out simple analyses of all sorts of investment science
situations, especially those related to real options, and to work
with examples in the text, Investment Science. The newest version
of the software is called LatticeMaker and it is located on the
investment science web site available for (free) downloading.
One of the most interesting
results of real options theory concerns the option to wait. Perhaps
surprisingly, it is sometimes best to delay a project even though
it currently has positive present value.
This phenomenon occurs in
situations of capital investment, switching of operations, and
other long-term projects.
A nice example was pointed
out to me on a recent trip to New York. There are a number of
parking lots in Manhattan on which large income-producing
structures (office buildings for example) could be built. The net
present value of conversion from a parking lot to a building is
positive, and there is no legal restriction against the process;
but the lots are not being converted. It is better to wait until
next year. In fact, next year it will be better to wait another
year. This can go on year after year. This phenomenon has been
studied in the real options literature under certain assumptions
regarding the growth rates of economic variables and the
uncertainty around those rates. However, the advantage of waiting
does not necessarily depend on the presence of uncertainty.
Sometimes it pays to wait even when all future prices are known;
and this can be illustrated with a simple analysis.
To focus our discussion let
us think in terms of the parking lot situation. Suppose that the
annual profit of the parking lot is currently A and that
this grows at a rate 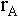 each year. Suppose also that a structure on the site would
produce a rental profit of B and this profit increases at a
rate of
each year. Suppose also that a structure on the site would
produce a rental profit of B and this profit increases at a
rate of 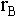 each year.
For simplicity let us assume that conversion can be carried out
immediately at a cost of S but this cost increases at a rate
of
each year.
For simplicity let us assume that conversion can be carried out
immediately at a cost of S but this cost increases at a rate
of 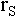 for every year
the project is delayed. Specific values we may wish to try are
A = $1 million, B = $10 million, S= $195
million, and the rates
for every year
the project is delayed. Specific values we may wish to try are
A = $1 million, B = $10 million, S= $195
million, and the rates
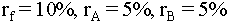
where 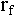 is the
risk-free rate at which to discount future cash flows.
is the
risk-free rate at which to discount future cash flows.
Note first that if the
parking lot is never converted, it will generate the revenue
stream
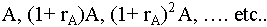
The present value of this kind of stream (where
the terms are discounted by
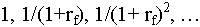
can be evaluated by a standard formula (the
Gordon formula) and its value is
.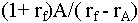
For the specific values we
gave, this is 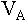 =$22 million. This is the present value if the
parking lot is never converted.
=$22 million. This is the present value if the
parking lot is never converted.
If a structure is
immediately erected on the lot, the revenue stream will
be
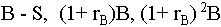
and so forth. The value of
this stream is evaluated the same way as the stream from the
parking lot and is
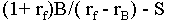
For our specific values this
is 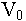 =$25 million. The value gained
by immediate conversion is
=$25 million. The value gained
by immediate conversion is
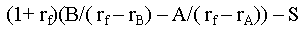
which for our example is $3
million.
Conversion has a higher
present value than non-conversion. In fact, we see that
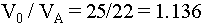
so the present value of
conversion is about 13% greater than that of the status quo.
Conventional analysis would dictate that the building should be
converted.
The key mathematics of this
example is simplest if we consider the benefit of waiting one year
to convert. Suppose, for example, that we wait one year instead of
converting at time 0. The difference in present value by
this delay is given by the simple formula
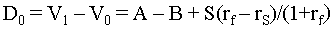
This formula is easy to understand. A delay
will give us A instead of B in the initial period, so
the net change is A - B. However, we also delay the
conversion cost. In discounted terms the cost would have been S but
with the delay it is
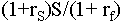
The difference is
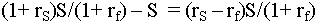
which we enter as a negative
since it is a cost.
In our example, this
produces 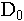 = $8.727 million-a huge difference considering that
the value of converting earlier is only $3 million.
= $8.727 million-a huge difference considering that
the value of converting earlier is only $3 million.
Pursuing this idea we can find the
relatively simple general formula for 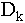 the difference between switching at k
and waiting until k + 1. The same logic gives
the difference between switching at k
and waiting until k + 1. The same logic gives
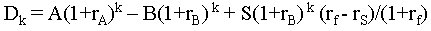
This formula could be used at each time to
determine if it is beneficial to convert or wait. We will come back
to this later, since it helps explain the numerical results we
shall obtain. It is possible to compute the various 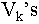 defined
as the present value for conversion at time k. They are
given by the (somewhat messy but still manageable) formula
defined
as the present value for conversion at time k. They are
given by the (somewhat messy but still manageable) formula
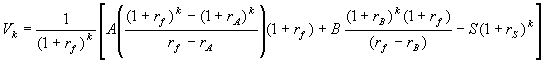
A graph of these values is shown below.
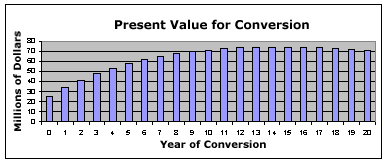
The maximum possible present
value is $73.883 million and is achieved by converting the parking
lot to an income-producing building in year 14.
At year 14, the present
value of going forward with the parking lot (using year 14 as the
starting point) is $43.56 million. The corresponding value for
going forward with the conversion is $240.58 million. Hence,
conversion is carried out when the present value of that project is
5.52 as great as the status quo. At time 0 we found that
conversion was worth 13% more than the status quo; that was not
nearly enough; we need a ratio of 5.52 to justify immediate
conversion.
The reason that one should
wait to convert is that waiting postpones cost, and since in our
example 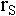 = 0, this postponement is valuable because of
discounting. This savings initially outweighs the increased cash
flow due to the structure. However, as time k increases, the
rent increases and the cost advantage to delay becomes small
compared to the difference in profit. This is clearly shown in the
equation for
= 0, this postponement is valuable because of
discounting. This savings initially outweighs the increased cash
flow due to the structure. However, as time k increases, the
rent increases and the cost advantage to delay becomes small
compared to the difference in profit. This is clearly shown in the
equation for 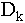 which shows that the term
involving B will for large k cause
which shows that the term
involving B will for large k cause 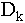 to become negative.
to become negative.
It is fun to consider the
case where 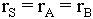 . Then if it is
advantageous to wait at time 0 it is advantageous to wait
every year---forever.
. Then if it is
advantageous to wait at time 0 it is advantageous to wait
every year---forever.
The conclusions of this
example are of course dependent of the values of the parameters.
And the advantage of waiting rapidly disappears if the total number
of years considered is not infinity. Hence, projects in fast-moving
industries may have short lives and should not be delayed.
Competition is another factor that may tend to favor immediate
action rather than delay.
The whole issue is more complex if there is
uncertainty with respect to, say, the profits. In this case there
may be an advantage to waiting, simply to see what these profits
will be. This, however, is another story. The main point of the
example presented here is that it may be valuable to wait even if
the present value of current action is positive.